How to Model Time Series in Python

In this article, we introduce two models to start modelling time series:

• random walk
• moving average process

This article is meant to be hands-on. So make sure to start you Jupyter notebook and follow along!

The complete notebook can be found here.

Let’s get started!

Dive deeper into time series with my free time series cheat sheet, covering statistical models, deep learning models, all implemented in Python!

Random Walk Model

The random walk model is expressed by this formula:

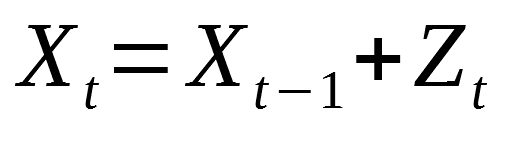
In words, it means that the location at the present time t is the sum of the previous location and noise, expressed by Z. Here, we assume that the noise is normally distributed (mean of 0 and variance of 1).

Of course, we start our random walk at 0, we can say that any point in time is the sum of all noise up to that time. Mathematically:

Let’s simulate a random walk in Python.

First, we will import all libraries that will be required for this part and the next section of this article:

from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.arima_process import ArmaProcess
from statsmodels.tsa.stattools import acf

import matplotlib.pyplot as plt
import numpy as np

%matplotlib inline

Then, we generate a dataset of 1000 data points. The starting point is 0, and we add random noise to the previous point to generate the next one:

steps = np.random.standard_normal(1000)
steps[0]=0
random_walk = np.cumsum(steps)

Plotting our dataset, we see the following:

plt.figure(figsize=[10, 7.5]); # Set dimensions for figure
plt.plot(random_walk)
plt.title("Simulated Random Walk")
plt.show()

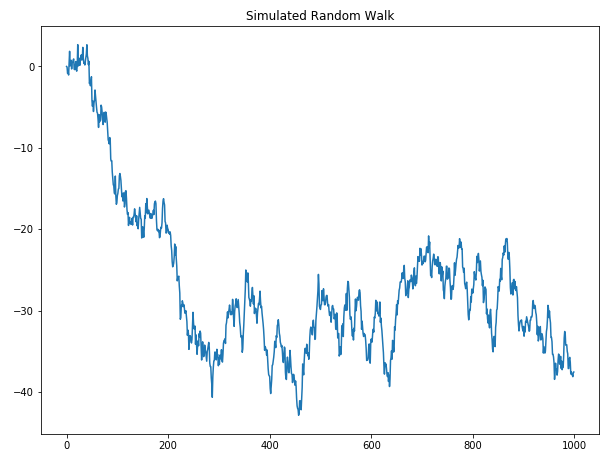
Now, your random walk might be different than the plot above, because the noise is well…random. Therefore, maybe your random walk is actually moving upwards through time.

Now, let’s take a look at the autocorrelation plot (or correlogram) of our random walk:

random_walk_acf_coef = acf(random_walk)
plot_acf(random_walk, lags=20);

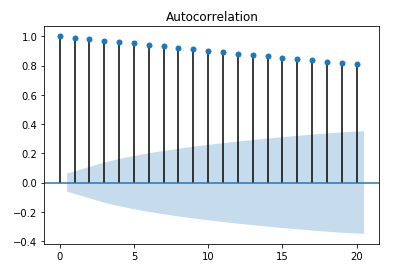
No matter what your random walk looks like, you should obtain a very similar correlogram. As you can see, even with a lag of 20, the correlation is very important. Therefore, the process is not stationary.

Now, everything points to the presence of a trend in our dataset. Would it be possible to remove this trend?

Yes!

Knowing that a random walk adds a random noise to the previous point, if we take the difference between each point with its previous one, we should obtain a purely random stochastic process.

Let’s verify that in Python. To take the difference, we do:

random_walk_diff = np.diff(random_walk, n=1)

Then, we plot the result and we should get:

plt.figure(figsize=[10, 7.5]); # Set dimensions for figure
plt.plot(random_walk_diff)
plt.title('Noise')
plt.show()

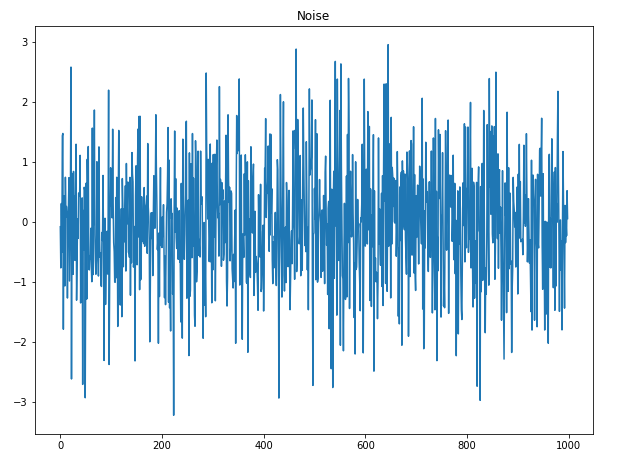
As you can see, the plot above has no systematic change in trend, variance, and it has no seasonality. Therefore, we definitely have a purely random process.

Looking at the correlogram of the difference:

plot_acf(random_walk_diff, lags=20);

We see that this is the correlogram of a purely random process, where the autocorrelation coefficients drop at lag 1.

Moving Average Process

Let’s start by gaining an intuition of what a moving average process is.

Suppose that you throw a rock in a pond of water and that you are tracking the position of a single water drop on the surface through time. Of course, when the rock hits the surface, ripples are formed, and so our drop will move up and down. Now, let’s suppose that ripples on the surface only last for two seconds, after which the surface comes back to being totally flat.

Then, we can say that the position of our water drop can be expressed as:

The equation above says that the position X at time t depends on the noise at time t, plus the noise at time t-1 (with a certain weight theta), plus some noise at time t-2 (with a certain weight).

This is called a moving average process of order 2, which can also be denoted as MA(2).

The generalized notation is MA(q). In the example above, q = 2.

Let’s simulate this process in Python.

Specifically, we will simulate the following process:

It is again a moving average process of order 2, but we specified the weights. Feel free to change them and experiment with the parameters.

We start by specifying the lag. Here, we are using a lag of 2.

ar2 = np.array([2])

Then, we specify the weights. In the present case, the weights are [1, 0.9, 0.3].

ma2 = np.array([1, 0.9, 0.3])

Finally, we simulate the process and generate a thousand data points:

MA2_process = ArmaProcess(ar2, ma2).generate_sample(nsample=1000)

Now, let’s visualize the process and its correlogram:

plt.figure(figsize=[10, 7.5]); # Set dimensions for figure
plt.plot(MA2_process)
plt.title('Moving Average Process of Order 2')
plt.show()

plot_acf(MA2_process, lags=20);

Again, since the noise is generated randomly, your graph is probably different than mine. However, the correlogram should be similar to the one below:

As you notice, the correlation is significant up to lag 2. Afterwards, the correlation is not significant anymore. This makes sense since we specified a formula with a lag of 2.

This means that you can infer the lag of a time series using the correlogram. If you see that after a specific lag q, the correlation is not significant, then you can model your time series as an MA(q) process.

That’s it! You now understand what a random walk is and how to simulate it. Also, you learned about moving average processes, how to model them, and most importantly, how to identify the order of your moving average process.

Learn more about time series with my free time series cheat sheet!

Cheers!

Support me

Enjoying my work? Show your support with Buy me a coffee, a simple way for you to encourage me, and I get to enjoy a cup of coffee! If you feel like it, just click the button below 👇